Математика — предмет, который учит задавать вопросы и искать на них ответы

Алик Шкловер — выпускник МФТИ, преподаватель школ «Летово» и «Интеллектуал», участник первого набора и выпускник программы «Новый учитель», куратор для новых участников. Алик зарекомендовал себя как талантливый учитель математики, который не только преподает предмет, но и оказывает методическую поддержку другим учителям. Мы попросили Алика рассказать о том, как он видит школьную математику.

Школьная математика — предмет, который учит задавать вопросы и искать на них ответы. Во-всяком случае, так должно быть. Однако иногда, по разным причинам, происходит иначе, и многие вопросы повисают в воздухе. Я попробовал собрать несколько таких вопросов. Некоторые из них очень простые, другие затрагивают основы математики. Но их объединяет одно: ответы на все эти вопросы должны прозвучать на уроке.

5 класс. На 0 делить нельзя. Почему?

Что означает эта фраза? Это законодательный запрет, табу или что-то другое? Для начала разберемся, что вообще значит «делить»? Например, почему 6:2=3. Математик скажет так: «Деление — это обратная операция к умножению». Эта фраза означает, что 6:2=3, так как 3*2=6. Разобравшись с этим, можно приступать к нарушению запретов. Итак, поделим, к примеру, 1 на 0. Мы должны получить какой-то результат. Назовем его X. 1:0=X. Но тогда, X*0=1, а таких чисел не бывает. При умножении на 0 всегда получается 0. Вот и все объяснение. На ноль не стоит делить не потому, что от этого кому-то будет плохо, а просто потому, что это не получится.

Внимательный читатель, возможно, заметил, что рассуждение выше не работает, если попытаться делить 0 на 0. В том, что будет в этом случае, можно разобраться самостоятельно.

6 класс. Почему (-1)*(-1)=1?

Попробуйте привести убедительные аргументы в пользу такого ответа, и вы потерпите фиаско. Важно понимать, что школьные присказки про то, что два минуса дружат и дают плюс — мнемонические правила, но не объяснения. В самом деле, в примере -5-3 два минуса категорически отказываются дружить. Легко можно объяснить, что (-3)*5=-15. Если воспринимать -3 как долг в три рубля, то ясно, что пяти людям я буду должен 15 рублей. А вот на случае двух отрицательных чисел начинает кипеть голова. Долг отрицательному числу людей? Путешествие назад во времени в обратном направлении? Другая интерпретация?

Так почему же (-1)*(-1)=1? Глубокий математический ответ звучит так: «Нам так захотелось». Мы долго жили с положительными числами, разработали правила общения с ними, а затем придумали новые числа — отрицательные. Это значит, что для них можем выбирать новые правила. Тогда почему нам захотелось, чтобы (-1)*(-1) был равен 1? Почему не -1? Или, например, не 42? Дело в том, что, введя новые числа, математики захотели сохранить старые правила: от перемены мест множителей произведение не меняется, при умножении любого числа на 0 получался 0, а еще сохраняется распределительный закон. Распределительный закон — это то, что позволяет умножать 56 на 3 в уме: 56 — это 50+6. 50*3=150, 6*3=18. Итого 150+18=168. На математическом языке это записывается так: 56*3=(50+6)*3=50*3+6*3=150+18=168. А в буквенном виде так: (a+b)*c=a*c+b*c.

Но вернемся к отрицательным числам. Пусть мы не знаем, чему равно (-1)*(-1), но хотим, чтобы сохранялись все старые законы. Попробуем вычислить (1+(-1))*(-1) двумя способами. С одной стороны, это 0, так как в скобках получается 0, а мы требуем, чтобы при умножении чего угодно на 0 получался 0. С другой стороны, если использовать распределительный закон, то получится 1*(-1)+(-1)*(-1). Первое слагаемое — это -1 (при умножении чего угодно на 1 получается само число). Тогда, если учитывать первый способ (-1+(-1)*(-1)=0), то (-1)*(-1)=1.

7 класс. Зачем доказывать очевидное?

В седьмом классе ученики начинают изучать новую науку — геометрию — и сразу сталкиваются с двумя новыми понятиями: аксиома и теорема. Аксиома, как учит Ералаш, — это истина, не требующая доказательств. А вот теорема, напротив, не может считаться таковой, если она не доказана.

Одна из аксиом гласит: «Через две точки можно провести прямую, причем только одну». Одна из теорем гласит: «Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную данной, притом только одну».

Кажется, что здравомыслящему человеку очевидны оба эти утверждения. Так почему же первое — аксиома, а второе — теорема? Чтобы понять это, обратимся к бытовому смыслу прямой. Здравый смысл подсказывает, что прямая — это результат соединения двух точек кратчайшим способом и продолжения того, что получилось. Если соединить точки зигзагом, выйдет намного длиннее. Посмотрим, что произойдет с таким пониманием прямой на шаре:

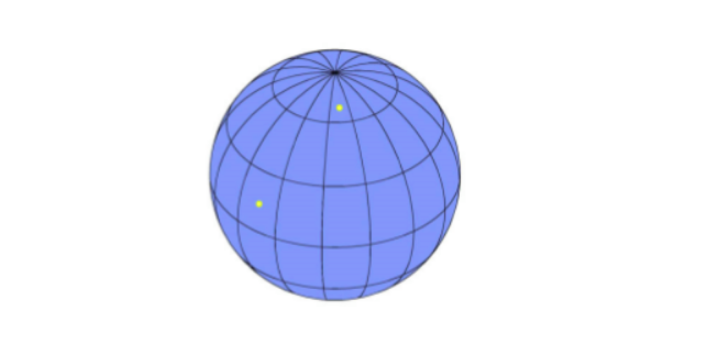
Возьмем на шаре две точки: северный и южный полюс. Как пройти между ними кратчайшим способом? Ясно, что надо идти по меридиану. То есть меридиан — аналог прямой на шаре. Но меридианов несколько. Значит, через две точки на шаре можно провести более одной прямой. Более того, каждый из этих меридианов — перпендикуляр еще одной прямой — экватору. То есть из северного полюса на экватор можно опустить сколько угодно перпендикуляров.

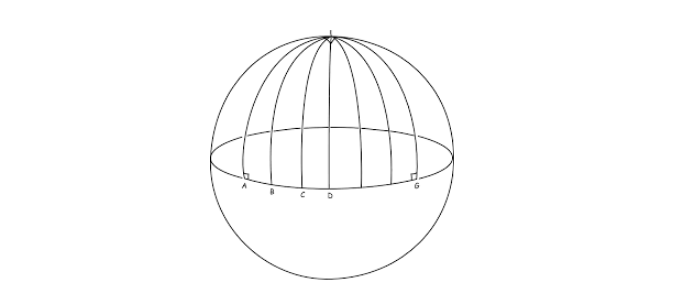
На шаре теорема о перпендикулярах оказалась не только неочевидной, но еще и неверной. В этом главный смысл геометрии: мы делаем несколько предположений, называемых аксиомами, и начинаем рассуждать, опираясь только на них. Аксиомы могут быть не более очевидны, чем другие теоремы. Важно понимать, что аксиомы — фундамент геометрии, на котором все строится. Сделаем другие предположения — получим другую геометрию.

8 класс. Почему корень из двух — иррациональное число?

Это математический вопрос, но он очень важен с точки зрения школьной программы. Если быть совсем точным, то расширенная версия этого вопроса звучит так: «Кто сказал, что корень из двух — новое число, а не дробь, которую мы изучали раньше? А если даже и новое число, то зачем мне его изучать? Не бывает же корня из двух сантиметров».
Начнем со второй части: корень из 2 см, как ни странно, бывает, и это то, что в свое время перевернуло мировоззрение пифагорейцев. Убедимся в этом. Для этого нарисуем по клеточкам следующую фигуру:

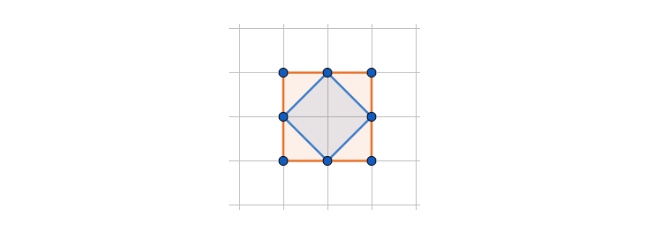
Площадь красного квадрата — 4. Синяя фигура — это тоже квадрат. Легко заметить, что синяя фигура по площади равна половине красной, то есть ее площадь — 2. Тогда у ее стороны должна быть такая длина a, что a²=2. Попробуем найти это число. 1 — слишком мало. 1²=1. 2 — слишком много, 2²=4. 1,4 даст нам 1,96, а 1,5²=2,25. Первого недостаточно, второе — перебор.

Мы можем стараться вычислять а все точнее и точнее, но правильного значения так и не получим. Не остается ничего, кроме как придумать для него специальный знак и написать так: a = корень из 2.

То, что написано выше, конечно, всего лишь иллюстрация, а не доказательство. Вдруг мы просто поленились и сделали слишком мало шагов, пытаясь найти число a? И на это есть строгий и удивительный, но достаточно сложный ответ. Пусть корень из двух можно представить в виде дроби: корень из 2=m/n. Договоримся, что m/n — несократимая дробь (иначе можно ее сократить и получить несократимую). Тогда, возводя в квадрат, получим: 2=m² / n². Это можно представить так: 2n²=m². Тогда m — четное число. Его можно записать в виде m=2k. Тогда 2n²=(2k)²=4k². Но тогда можно разделить на 2, и получится, что n²=2k². То есть n — тоже четное число! Но такого не может быть, ведь в этом случае дробь m/n можно было бы сократить. Значит, корень из 2 нельзя представить в виде дроби.

9 класс. Что такое вероятность?

Согласно известной шутке, вероятность встретить динозавра — 50%: либо встретишь, либо нет. Но никто из нас динозавров не встречал, а это значит, что вероятность существенно ниже. Однако, если заменить встречу с динозавром на выпадение решки в броске монетки, то рассуждение становится вполне логичным. Так в чем же ошибка? Чтобы ответить на этот вопрос, обсудим, что такое вероятность.

Надо отметить, что вероятность всегда была сложным вопросом для человечества. Задачи на вероятность человечество решает не одну сотню лет. Но стать наукой теория вероятностей смогла только недавно, а именно в ХХ веке. Это случилось во многом благодаря великому ученому ХХ века Андрею Николаевичу Колмогорову в тот момент, когда он дал строгий ответ на главный вопрос. Ответ, данный Колмогоровым, слишком сложен, поэтому ограничимся более ранними представлениями.

Рассмотрим такую задачу. Бросаем две монеты. Какова вероятность, что на одной решка, а на другой орел? У подобного броска три исхода: две решки, орел с решкой и два орла. Значит, вероятность орла с решкой — 1/3. Однако простой эксперимент, который можно провести дома (и уж точно стоит провести с детьми в классе), показывает: при большом числе бросков примерно в половине случаев выпадают орел с решкой.

В чем ошибка? В том, что три выписанных нами исхода не равновероятны. Мы «склеили» два случая: орел на первой монете, а решка на второй и наоборот. Та же ошибка допущена и в шутке про динозавра, здесь равновероятными считаются исходы «встретить» и «не встретить».

Но как понять, какие события равновероятны, а какие нет? Вообще говоря, никак. Равновероятность событий — то, что должно содержаться в условии задачи. Например, считая, что вероятность встретить динозавра — 50 %, математик вполне сможет решить задачу о среднем количестве динозавров, которых он встретит по дороге.

Теория вероятностей — наука, в которой эксперимент встречается с логикой. Экспериментаторы подсказывают, какие события считать равновероятными, а математик, пользуясь этими данными, сообщает количество динозавров по дороге на работу. Если не сообщить математику, какие исходы равновероятны, то можно попасть в беду.

Старшая школа: Зачем нужен интеграл?

Если вам не повезло со школьным учителем, то вряд ли в школе вам сообщили о интегралах что-то кроме того, как их считать. Если учитель был знающим, то он добавил, что интеграл — это площадь под графиком. Однако на вопрос о том, кому это может потребоваться, вы вряд ли получили ответ. Врать не буду, интеграл — не то, что нужно в жизни каждому человеку. Но я хочу объяснить, зачем нужен интеграл математику.

Давайте забудем все формулы интегрирования и ограничимся простым определением: интеграл функции — это площадь под ее графиком. Речь идет об интегрировании на отрезке. Возьмем самый простой случай: вы шли 2 часа со скоростью 5 км в час. График скорости в этом случае очень простой:

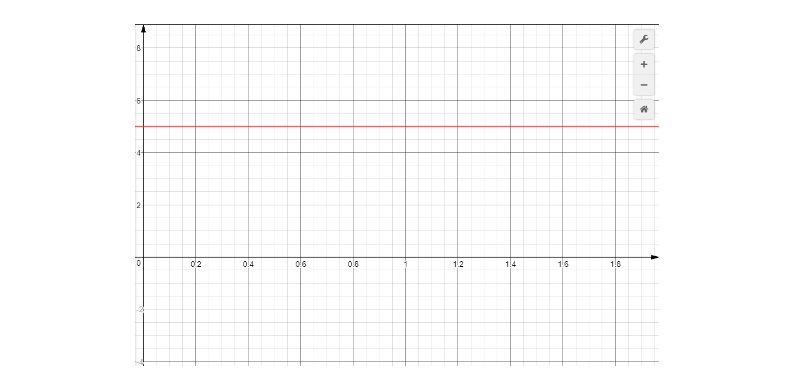
Посчитаем интеграл, то есть площадь под графиком. Умножаем стороны прямоугольника, пять на два — это 10. Кстати, ровно столько километров вы и прошли! Другой пример: автомобиль разогнался за минуту до 1 км/м, а дальше минуту ехал с этой скоростью.

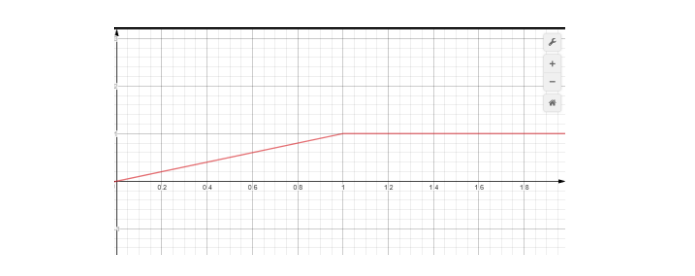
Площадь под графиком — половина прямоугольника 1 на 1, плюс еще такой прямоугольник. Общая площадь — 1,5. И снова это то расстояние, которое проехал автомобиль, но теперь мы уже не можем найти это арифметическими действиями.

Интеграл от графика скорости — всегда длина пройденного пути, даже если это распечатанный график скорости из приложения для бега. Это только одно самое простое применение интеграла. Без интеграла невозможно вычислить объем шара (объем — это интеграл от площади сечения), выпавший объем осадков — интеграл от интенсивности дождя, а масса предмета — интеграл от его плотности. Я не очень понимаю, почему интеграл включен в школьную программу. Но уж если он там есть, то пусть будет там так, чтобы у ученика оставалось нечто большее, чем просто причудливый знак.

Главное удовольствие в изучении математики — это возможность сомневаться, задаваться вопросами, искать на них ответ и быть правым не потому, что ссылаешься на чье-то мнение, а потому что у тебя есть доказательство. Но это удовольствие нужно научить получать. Нужно задавать вопросы. Нужно поощрять детей искать ответы. Нужно, чтобы самим детям было не страшно подвергнуть чужие слова сомнению. А для того, чтобы это случилось, ученикам нужно много хороших учителей. И если в школе на уроке математики вас всегда волновал вопрос «почему?», если, читая эти вопросы, выше вы радовались, что больше людей узнает на них ответы, да даже просто если вам было приятно узнать новый для себя математический факт, то, возможно, один из этих учителей — вы.